Equilíbrio de ponto material

Olá pessoal! O Direto ao ponto tem como objetivo apresentar a teoria para aqueles que não querem perder tempo e precisam de um resumo de Física rápido da matéria. Vamos lá!

 

1. EQUILÍBRIO DE PONTO MATERIAL

Um ponto material não leva em consideração as dimensões do objeto.

 

1.1 Um lustre pendurado no teto

Considere um lustre pendurado no teto. As forças que atuam sobre o lustre são o seu peso e a normal.

 

O somatório vetorial das forças deve ser nulo para que o lustre permaneça em equilíbrio estático.

 

 

Na prática, quando apenas duas forças atuam sobre o corpo em uma mesma direção, os seus módulos são iguais. No exemplo do lustre, o módulo da força peso é igual ao módulo da força de tração.

 

 

1.2 Quadro pendurado (mesmo ângulo)

O quadro abaixo está pendurado por um barbante em um prego. O ângulo que cada parte do barbante faz com a horizontal é de 45 graus em ambos os lados. Isso facilita a resolução do problema.

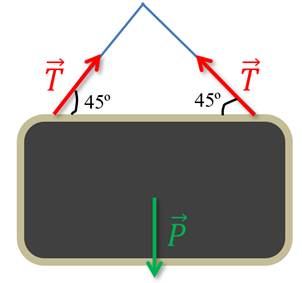
A força de tração pode ser projetada nos eixos x (T_X) e y (T_Y). Para simplificar a ilustração, consideramos o quadro como um ponto material.

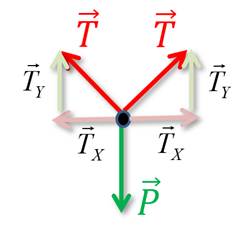
Repare que existe uma diferença desta situação para o caso do lustre pendurado. Existiam apenas forças atuando sobre o lustre na direção vertical. No quadro, entretanto, existem componentes das forças nos eixos x e y. A resultante das forças deve ser nula em cada eixo para que o quadro permaneça em equilíbrio estável.

 

·        Horizontal (eixo x): a resultante é nula, pois as componentes T_X são iguais.

 

·        Vertical (eixo y): o somatório das componentes T_Y é igual a 2T_Y, que é igual a força peso P do quadro.

 

 

Considere que o lustre tenha 10 kg de massa (Peso = 100 N) e cos 45º = sen 45º ≈ 0,7.

 

 

A tração T em cada parte do barbante vale: