Espelhos Esféricos – Equação de Gauss

1. A MATEMÁTICA DOS ESPELHOS ESFÉRICOS

O eixo do x é o eixo das distâncias e o eixo do y é o eixo dos tamanhos (do objeto e da imagem).

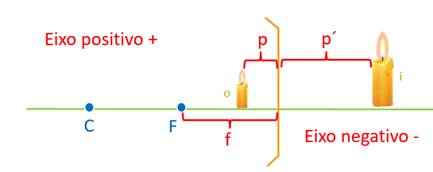
Os objetos e as imagens reais então do mesmo lado no qual a luz incide, ou seja, estão do mesmo lado da superfície refletora. Os objetos e as imagens virtuais encontram-se em lados opostos. Observando o referencial, notamos que distâncias reais são positivas e que distâncias virtuais são negativas.

 

Adotamos as convenções de sinais abaixo para a distância do objeto ao espelho (p) e para a distância da imagem ao espelho.

 

• p´ > 0 – imagem real
• p´ < 0 – imagem virtual

 

Observe a convenção de sinais para o tamanho da imagem (i).

 

• i > 0 – imagem direita
• i < 0 – imagem invertida

 

O espelho côncavo possui foco real (na frente do espelho) e a sua distância focal (f) é positiva. O espelho convexo possui foco virtual (atrás do espelho) e sua distância focal (f) é negativa.

 

• f > 0 – côncavo
• i < 0 – convexo

 

1.1. Equação de Gauss

A equação de Gauss relaciona a distância focal do espelho (f) e as distâncias do objeto (p) e da imagem (p´) ao espelho.

 

 

1.2 Aumento Linear (A)

O aumento linear transversal é um número que compara o tamanho da imagem (i) formada com o tamanho do objeto (o).