Energia
Olá pessoal! O Direto ao ponto tem como objetivo apresentar a teoria para aqueles que não querem perder tempo e precisam de um resumo de Física rápido da matéria. Vamos lá!
1. INTRODUÇÃO
Podemos definir a energia como a capacidade que um corpo possui em realizar trabalho.
A seguir, resumimos os principais tipos de energia encontrados na natureza.
· Energia cinética: associada a velocidade de um corpo. Um projétil é inofensivo, porém quando lançado com uma velocidade grande através de uma arma, se torna devastador.
· Energia potencial gravitacional: associada a altura que um corpo se encontra. Uma pedra que cai do alto de um prédio pode causar sérios danos a um carro no solo.
· Energia elástica: energia associada a sistema que se deformam, tal como molas ou elásticos.
2. ENERGIA CINÉTICA
A energia cinética de um corpo pode ser calculada pela expressão abaixo.
\({E_C} = \frac{{m{v^2}}}{2}\)
A unidade de energia é o Joule (J).
\(\left| {{E_C}} \right| = \frac{{\left| m \right|\left| {{v^2}} \right|}}{2} = \frac{{kg,{m^2}}}{{{s^2}}}\)
· Energia cinética é diretamente proporcional ao quadrado da velocidade de um corpo.
3. ENERGIA POTENCIAL GRAVITACIONAL
A expressão abaixo é usada para calcular a energia potencial gravitacional de um corpo.
\({E_P} = mgh\)
A energia potencial gravitacional depende de três fatores: da massa (m) do objeto, da aceleração da gravidade (g) e da altura (h) em que o corpo se encontra em relação a um ponto de referência.
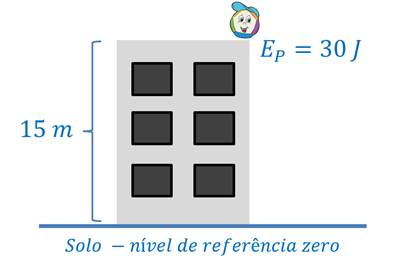
Para determinar a energia potencial gravitacional de um corpo, é necessário estabelecer um nível de referência. No exemplo abaixo, a pedra de massa 200 gramas está localizada no topo de um prédio de 15 metros de altura em relação ao solo (nível de referência). Portanto, essa pedra possui 30 J de energia potencial gravitacional.
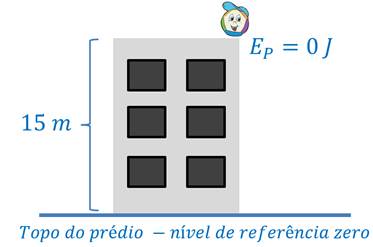
Porém, podemos escolher o nível de referência no topo do prédio. Nesse caso, a altura da pedra em relação a esse nível de referência é nula, assim como a sua energia potencial gravitacional.
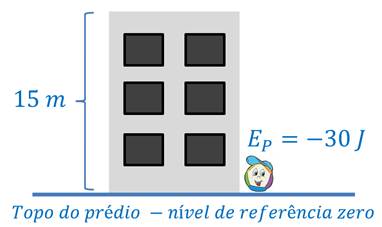
Agora considere a pedra no solo. Mantido o nível de referência zero no topo de prédio, a energia potencial gravitacional da pedra é de – 30 J.
4. ENERGIA POTENCIAL ELÁSTICA
A energia potencial elástica é a energia armazenada em molas comprimidas ou esticadas em relação ao seu ponto de equilíbrio.
A fórmula para o cálculo desta energia é:
\({E_P} = \frac{{k{x^2}}}{2}\)
Onde:
k à constante elástica da mola (dureza da mola).
x à deformação da mola. O quanto a mola é esticada ou comprimida em relação a posição de equilíbrio (x = 0 – posição de relaxamento).
5. ENERGIA MECÂNICA
A energia mecânica de um corpo é o somatório da energia cinética mais a energia potencial (gravitacional e elástica) em um determinado ponto.
\({E_{MEC}} = {E_C} + {E_P}\)
6. TEOREMA TRABALHO-ENERGIA CINÉTICA
Considere uma força \(\vec F\) aplicada a uma bola de futebol com velocidade inicial v0. A bola se desloca ∆s e atinge a velocidade final v.
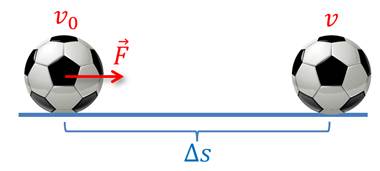
A energia necessária (trabalho) para aumentar a energia cinética da bola está relacionada pelo teorema trabalho-energia cinética.
7. CONSERVAÇÃO DA ENERGIA MECÂNICA
Em sistemas onde atuam apenas forças conservativas, a energia mecânica se conserva durante toda a trajetória. A força peso, a normal e a força elástica são exemplos de forças conservativas, ou seja, o trabalho não depende da trajetória. Esse tipo de força não é capaz de transformar energia mecânica em outro tipo de energia.
· A energia mecânica de um corpo permanece constante se atuam apenas forças conservativas sobre ele durante a sua trajetória.
7.1 Transformando energia mecânica em térmica
O atrito e a resistência do ar são considerados forças dissipativas pois transformam energia mecânica em energia térmica (calor), realizando um trabalho resistente. A energia total do sistema se conserva, porém, a energia mecânica não. Nos sistemas dissipativos, não é possível escrever a expressão:
\({E_{MEC\left( {INICIAL} \right)}} = \;{E_{MEC\left( {FINAL} \right)}}\)
Portanto, o trabalho das forças dissipativas será a diferença entre a energia mecânica final e inicial.
\(W = {E_{C\left( {FINAL} \right)}} – {E_{C\left( {INICIAL} \right)}}\)
