Acústica
Olá pessoal! O Direto ao ponto tem como objetivo apresentar a teoria para aqueles que não querem perder tempo e precisam de um resumo de Física rápido da matéria. Vamos lá!
1. INTERFERÊNCIA DE ONDAS EM UMA DIMENSÃO
Uma vibração é estacionária quando a fonte produz pulsos constantemente. Esses pulsos sofrem interferência.
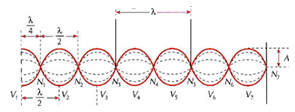
Os pontos de máxima interferência construtiva são chamados de ventre (V) e onde a interferência é mínima, os pontos são chamados de nó (os pontos não oscilam).
2. CORDAS VIBRANTES
Existem duas formas de vibração de cordas: presas nas duas extremidades ou preso em uma extremidade apenas.
2.1 Corda presa em duas extremidades
A corda está presa nas duas extremidades. O primeiro modo de vibração é chamado de modo fundamental ou 1ª harmônico, o segundo modo de vibração é chamado de 2ª harmônico, o terceiro modo de vibração é chamado de 3ª harmônico e assim por diante, como mostra a figura abaixo.
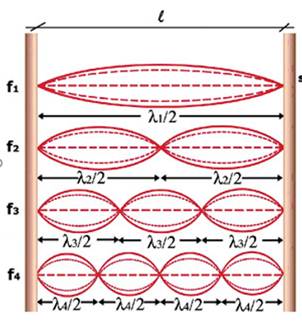
Como podemos observar, a ilustração mostra a relação do comprimento de onda com o comprimento da corda dependendo do modo de vibração, essa relação pode ser expressa por:
\(\lambda = \frac{{2L}}{n}\)
onde n = 1, 2, 3, … representam os respectivos harmônicos.
\(f = \frac{{nv}}{{2L}}\)
n = 1, 2, 3, …
2.2 Corda presa em uma extremidade e solta na outra
Esse caso é raro. O primeiro harmônico é formado apenas pela metade de uma figura de ressonância.
A fórmula vale:
\(f = \frac{{nv}}{{4L}}\)
n = 1, 3, 5…
3. TUBOS SONOROS
Existem dois tipos de tubos sonoros: abertos e fechados. Em um tubo, o ar no seu interior entra em ressonância.
3.1 Tubo aberto
O tubo aberto possui as duas extremidades abertas. A figura a seguir ilustra os modos de ressonância. Repare que no primeiro harmônico, existem duas figuras de ressonância pela metade que forma uma figura inteira. Por isso, a fórmula para o cálculo da frequência é a mesma da corda presa nas duas extremidades.
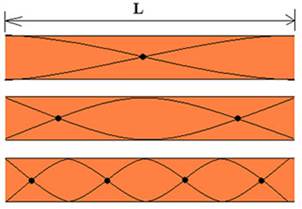
\(f = \frac{{nv}}{{2L}}\)
n = 1, 2, 3, …
3.2 Tubo fechado
O tubo fechado possui uma extremidade aberta e uma fechada. Repare que a primeira figura de interferência é a metade de uma ressonância completa.
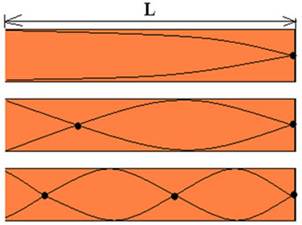
O tubo fechado se comporta como uma corda presa em uma extremidade. Portanto, a fórmula para o cálculo da frequência vale:
n = 1, 3, 5…
